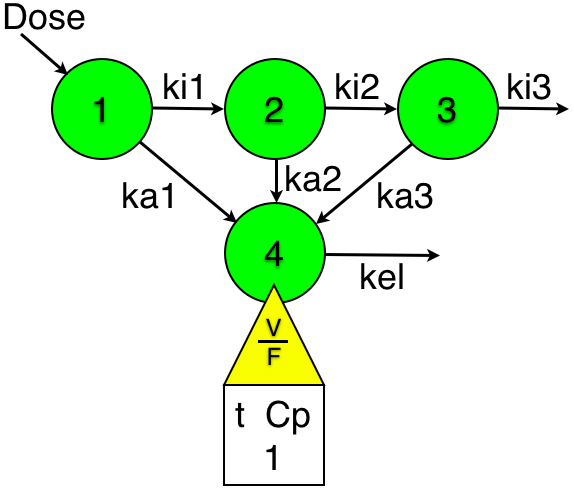
One compartment Model (Dose,ki1-3,ka1-3/kel/V/F)

One compartment Model (Dose,ki1-3,ka1-3/kel/V/F)
--
Boomer Batch File
2 wls,bayes,sim,irwls,sim+error,grid
1 Screen, diskfile
onec_cs <- output to onec_cs.OUT
1 Parameter type <- start of Dose input, type 1
Dose
100.0 Parameter value
1 To
0 happy or not
2 Parameter type <- start of ki1 input, type 2
ki1
1.200 Parameter value
2 To <- into component 2 (small intestine ?)
1 From <- from component 1 (stomach ?)
0 happy or not
2 Parameter type <- start of ki2, type 2
ki2
0.6000 Parameter value
3 To <- into component 3 (large intestine ?)
2 From
0 happy or not
2 Parameter type <- start of ki3, type 2
ki3
0.3000 Parameter value
0 To <- to outside model
3 From
0 happy or not
2 Parameter type <- start of ka1, type 2
ka1
0.2000 Parameter value
4 To <- into central compartment
1 From <- from component 1 (stomach ?)
0 happy or not
2 Parameter type
ka2
1.500 Parameter value
4 To
2 From
0 happy or not
2 Parameter type
ka3
0.4000 Parameter value
4 To
3 From
0 happy or not
2 Parameter type
kel
0.1500 Parameter value
0 To
4 From
0 happy or not
18 Parameter type
V/F
12.30 Parameter value
1 To
[Drug]
4 From
0 happy or not
18 Parameter type <- start of parameter One-1 used to
One-1 provide amount in component 1
1.000 Parameter value
2 To
Amt 1
1 From
0 happy or not
18 Parameter type <- start of parameter One-2 used to
One-2 provide amount in component 2
1.000 Parameter value
3 To
Amt 2
2 From
0 happy or not
18 Parameter type
One-3
1.000 Parameter value
4 To
Amt 3
3 From
0 happy or not
18 Parameter type
One-4
1.000 Parameter value
5 To
Amt 4
4 From
0 happy or not
-1 Parameter type
2 Integration method
0.000 Relative error
0.000 Absolute error
Simulation - Oral dose with three absorption sites
1 Data from disk or keyboard
0.000 X value
0.000 Y value
1.000 X value
0.000 Y value
2.000 X value
0.000 Y value
3.000 X value
0.000 Y value
4.000 X value
0.000 Y value
6.000 X value
0.000 Y value
9.000 X value
0.000 Y value
12.00 X value
0.000 Y value
-1.000 X value
0 Accept, correct, delete, insert, of
0 Continue or save data
0.000 X value
0.000 Y value
1.000 X value
0.000 Y value
2.000 X value
0.000 Y value
3.000 X value
0.000 Y value
4.000 X value
0.000 Y value
6.000 X value
0.000 Y value
9.000 X value
0.000 Y value
12.00 X value
0.000 Y value
-1.000 X value
0 Accept, correct, delete, insert, of
0 Continue or save data
0.000 X value
0.000 Y value
1.000 X value
0.000 Y value
2.000 X value
0.000 Y value
3.000 X value
0.000 Y value
4.000 X value
0.000 Y value
6.000 X value
0.000 Y value
9.000 X value
0.000 Y value
12.00 X value
0.000 Y value
-1.000 X value
0 Accept, correct, delete, insert, of
0 Continue or save data
0.000 X value
0.000 Y value
1.000 X value
0.000 Y value
2.000 X value
0.000 Y value
3.000 X value
0.000 Y value
4.000 X value
0.000 Y value
6.000 X value
0.000 Y value
9.000 X value
0.000 Y value
12.00 X value
0.000 Y value
-1.000 X value
0 Accept, correct, delete, insert, of
0 Continue or save data
0.000 X value
0.000 Y value
1.000 X value
0.000 Y value
2.000 X value
0.000 Y value
3.000 X value
0.000 Y value
4.000 X value
0.000 Y value
6.000 X value
0.000 Y value
9.000 X value
0.000 Y value
12.00 X value
0.000 Y value
-1.000 X value
0 Accept, correct, delete, insert, of
0 Continue or save data
1 AUC line number
0 AUC line number
2 Continue,save,plot,supplemental,sen
-1 wls,bayes,sim,irwls,sim+error,grid <- finish
--
When you open onec_cs.OUT you should see the information below
** FINAL OUTPUT FROM Boomer (v3.3.6a) ** 5 July 2011 --- 1:26:20 pm
Title: Simulation -
Input: From onec_cs.BAT
Output: To onec_cs.OUT
Data for [Drug] came from keyboard (or ?.BAT)
Data for Amt 1 came from keyboard (or ?.BAT)
Data for Amt 2 came from keyboard (or ?.BAT)
Data for Amt 3 came from keyboard (or ?.BAT)
Data for Amt 4 came from keyboard (or ?.BAT)
Fitting algorithm: Simulation
Numerical integration method: 2) Fehlberg RKF45
with 4 de(s)
With relative error 0.1000E-03
With absolute error 0.1000E-03
This simulation took 0.1000E-01 seconds
Model and Parameter Definition
# Name Value Type From To Dep Start Stop
1) Dose = 100.0 1 0 1 0 0 0
2) ki1 = 1.200 2 1 2 0 0 0
3) ki2 = 0.6000 2 2 3 0 0 0
4) ki3 = 0.3000 2 3 0 0 0 0
5) ka1 = 0.2000 2 1 4 0 0 0
6) ka2 = 1.500 2 2 4 0 0 0
7) ka3 = 0.4000 2 3 4 0 0 0
8) kel = 0.1500 2 4 0 0 0 0
9) V/F = 12.30 18 4 1 0 0 0
10) One-1 = 1.000 18 1 2 0 0 0
11) One-2 = 1.000 18 2 3 0 0 0
12) One-3 = 1.000 18 3 4 0 0 0
13) One-4 = 1.000 18 4 5 0 0 0
Data for [Drug] :-
DATA # Time Observed Calculated (Weight) Weighted residual
1 0.000 0.00000 0.00000 0.00000 0.00000
2 1.000 0.00000 3.29360 0.00000 -0.00000
3 2.000 0.00000 4.91270 0.00000 -0.00000
4 3.000 0.00000 5.04374 0.00000 -0.00000
5 4.000 0.00000 4.65281 0.00000 -0.00000
6 6.000 0.00000 3.61161 0.00000 -0.00000
7 9.000 0.00000 2.33839 0.00000 -0.00000
8 12.00 0.00000 1.49516 0.00000 -0.00000
Data for Amt 1 :-
DATA # Time Observed Calculated (Weight) Weighted residual
1 0.000 0.00000 100.000 0.00000 -0.00000
2 1.000 0.00000 24.6597 0.00000 -0.00000
3 2.000 0.00000 6.08095 0.00000 -0.00000
4 3.000 0.00000 1.49948 0.00000 -0.00000
5 4.000 0.00000 0.369749 0.00000 -0.00000
6 6.000 0.00000 0.224660E-01 0.00000 -0.00000
7 9.000 0.00000 0.332408E-03 0.00000 -0.00000
8 12.00 0.00000 0.466057E-05 0.00000 -0.00000
Data for Amt 2 :-
DATA # Time Observed Calculated (Weight) Weighted residual
1 0.000 0.00000 0.00000 0.00000 0.00000
2 1.000 0.00000 21.2815 0.00000 -0.00000
3 2.000 0.00000 7.85414 0.00000 -0.00000
4 3.000 0.00000 2.25596 0.00000 -0.00000
5 4.000 0.00000 0.595360 0.00000 -0.00000
6 6.000 0.00000 0.379431E-01 0.00000 -0.00000
7 9.000 0.00000 0.569024E-03 0.00000 -0.00000
8 12.00 0.00000 0.798936E-05 0.00000 -0.00000
Data for Amt 3 :-
DATA # Time Observed Calculated (Weight) Weighted residual
1 0.000 0.00000 0.00000 0.00000 0.00000
2 1.000 0.00000 9.24588 0.00000 -0.00000
3 2.000 0.00000 10.2836 0.00000 -0.00000
4 3.000 0.00000 6.92829 0.00000 -0.00000
5 4.000 0.00000 3.94087 0.00000 -0.00000
6 6.000 0.00000 1.06894 0.00000 -0.00000
7 9.000 0.00000 0.134404 0.00000 -0.00000
8 12.00 0.00000 0.165019E-01 0.00000 -0.00000
Data for Amt 4 :-
DATA # Time Observed Calculated (Weight) Weighted residual
1 0.000 0.00000 0.00000 0.00000 0.00000
2 1.000 0.00000 40.5113 0.00000 -0.00000
3 2.000 0.00000 60.4263 0.00000 -0.00000
4 3.000 0.00000 62.0380 0.00000 -0.00000
5 4.000 0.00000 57.2296 0.00000 -0.00000
6 6.000 0.00000 44.4228 0.00000 -0.00000
7 9.000 0.00000 28.7622 0.00000 -0.00000
8 12.00 0.00000 18.3905 0.00000 -0.00000
Calculation of AUC and AUMC based on trapezoidal rule
AUC and AUMC for [Drug] using Calculated data
Time Concentration AUC AUMC
0.00000 0.00000
1.00000 3.29360 1.64680 1.64680
2.00000 4.91270 5.74995 8.20630
3.00000 5.04374 10.7282 20.6846
4.00000 4.65281 15.5764 37.5558
6.00000 3.61161 23.8409 77.8367
9.00000 2.33839 32.7659 141.909
12.0000 1.49516 38.5162 200.391
48.5457 388.023
AUC and AUMC extrapolated
from the last data point 20.7 % 48.4 %
Secondary Parameters
MRT = 7.9929
Half-life values for each first order rate constant
Parameter 2 has a half-life of ki1 is 0.578
Parameter 3 has a half-life of ki2 is 1.16
Parameter 4 has a half-life of ki3 is 2.31
Parameter 5 has a half-life of ka1 is 3.47
Parameter 6 has a half-life of ka2 is 0.462
Parameter 7 has a half-life of ka3 is 1.73
Parameter 8 has a half-life of kel is 4.62
Dose/AUC (= Clearance/F)
Parameter 1 gives Dose/AUC (CL/F) of 2.06
Calculation of AUC and AUMC using Method 9 of R.D. Purves
AUC and AUMC for [Drug] using Calculated data
Time Concentration AUC AUMC
0.00000 0.00000
1.00000 3.29360
2.00000 4.91270 6.02903 7.66660
3.00000 5.04374 11.1364 20.4460
4.00000 4.65281 15.9821 37.3732
6.00000 3.61161 24.2026 78.1290
9.00000 2.33839 32.9897 143.080
12.0000 1.49516 38.6460 201.842
48.6755 389.474
AUC and AUMC extrapolated
from the last data point 20.6 % 48.2 %
Secondary Parameters
MRT = 8.0014
Half-life values for each first order rate constant
Parameter 2 has a half-life of ki1 is 0.578
Parameter 3 has a half-life of ki2 is 1.16
Parameter 4 has a half-life of ki3 is 2.31
Parameter 5 has a half-life of ka1 is 3.47
Parameter 6 has a half-life of ka2 is 0.462
Parameter 7 has a half-life of ka3 is 1.73
Parameter 8 has a half-life of kel is 4.62
Dose/AUC (= Clearance/F)
Parameter 1 gives Dose/AUC (CL/F) of 2.05
Plots of observed (*) and calculated values (+)
versus time for [Drug] . Superimposed points (X)
5.044 Linear 5.044 Semi-log
| + | +
| + | +
| | +
| + |
| |
| |
| |
| |
| |
| + | +
| |
| + | +
| |
| |
| |
| |
| |
| + |
| |
| | +
| |
| |
| + |
| |
| |
| |
| |
| |
| |
| |
|X * * * * * * * | +
|_____________________________________ |X__*__*__*__*_____*________*________*
0.000 1.495
0 <--> 12. 0 <--> 12.
Plots of observed (*) and calculated values (+)
versus time for Amt 1 . Superimposed points (X)
100.0 Linear 100.0 Semi-log
|+ |+
| |
| |
| | +
| |
| | +
| |
| |
| | +
| |
| | +
| |
| |
| |
| |
| | +
| |
| |
| |
| |
| |
| |
| |
| + | +
| |
| |
| |
| |
| |
| + |
|* * * X X X X X | +
|_____________________________________ |*__*__*__*__*_____*________*________*
0.000 0.4661E-05
0 <--> 12. 0 <--> 12.
Plots of observed (*) and calculated values (+)
versus time for Amt 2 . Superimposed points (X)
21.28 Linear 21.28 Semi-log
| + | +
| |
| |
| | +
| |
| | +
| |
| |
| | +
| |
| |
| |
| |
| | +
| |
| |
| |
| |
| |
| + |
| |
| |
| | +
| |
| |
| |
| |
| + |
| |
| |
|X * * * X X X X | +
|_____________________________________ |X__*__*__*__*_____*________*________*
0.000 0.7989E-05
0 <--> 12. 0 <--> 12.
Plots of observed (*) and calculated values (+)
versus time for Amt 3 . Superimposed points (X)
10.28 Linear 10.28 Semi-log
| |
| + | + +
| | +
| |
| + |
| | +
| |
| |
| |
| |
| + |
| | +
| |
| |
| |
| |
| |
| |
| |
| + |
| |
| | +
| |
| |
| |
| |
| |
| + |
| |
| |
|X * * * * * X X | +
|_____________________________________ |X__*__*__*__*_____*________*________*
0.000 0.1650E-01
0 <--> 12. 0 <--> 12.
Plots of observed (*) and calculated values (+)
versus time for Amt 4 . Superimposed points (X)
62.04 Linear 62.04 Semi-log
| + | +
| + | +
| | +
| + |
| |
| |
| |
| |
| |
| + | +
| |
| + | +
| |
| |
| |
| |
| |
| + |
| |
| | +
| |
| |
| + |
| |
| |
| |
| |
| |
| |
| |
|X * * * * * * * | +
|_____________________________________ |X__*__*__*__*_____*________*________*
0.000 18.39
0 <--> 12. 0 <--> 12.