Chapter 6 Intravenous Infusion

return to the Course index
previous | next

Continuous IV Infusion - Steady State

The Model

Giving the drug by infusion changes the drug concentration versus time curve. The equations used to describe the drug concentration are different.

The model can be described schematically.

Figure 6.2.1 Scheme for One Compartment Intravenous Infusion

In Figure 6.2.1 we have added an infusion rate constant, k0, to the diagram presented earlier, (Figure 4.4.1). This is a zero order process so the units of k0 are amount per time, for example 25 mg/min.

Differential and Integrated equation

The differential equation for V • Cp is then:

Equation 6.2.1 Differential Equation for Drug amount During an IV Infusion

Equation 6.2.1 is the differential equation during the infusion period and it can be integrated to give Equation 6.2.2 using Laplace transforms.

Equation 6.2.2 Integrated Equation for Drug Amount in the body versus Time

and after dividing both sides by the apparent volume of distribution, V.

Equation 6.2.3 Integrated Equation for Drug Concentration versus Time

Equation 6.2.3 can be used estimate the drug concentration at various times after an infuion is started OR to calculate the infusion rate needed to achive a desired drug concentration.

Javascript Calculators using Equation 6.2.3

Calculator 6.2.1 Calculate Cp Given k0, kel and V at time t

Calculator 6.2.2 Calculate k0 required to give Cp at time t

You may notice that Equation 6.2.3 for Cp is quite similar to Equation 5.3.4 that we used before for the cumulative amount of drug excreted into urine. As you might expect the plot of Cp would be similar in shape.

Continuous Infusion k0 = 100 mg/hr, V = 20 L, kel = 0.2 hr^{-1

Figure 6.2.2 Linear Plot of Cp versus Time During a Continuous Infusion}

Click on the figure to view the interactive graph

If we continue the infusion indefinitely then we will approach a steady state plasma concentration when the rate of infusion will be equal to the rate of elimination.

This is because the rate of infusion is constant whereas the rate of elimination will increase as the plasma concentration increases. At steady state the two rates become equal. We can determine the steady state concentration from the differential equation by setting the rate of change of Cp, i.e. dCp/dt = 0.

Then

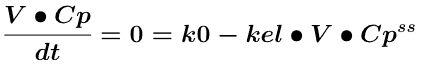
therefore

Equation 6.2.4 Steady State Concentration after Continuous IV Infusion

This could also be calculated from the integrated equation by setting e^{- kel • t} = 0 at t = ∞.

We can now calculate the infusion rate necessary to produce some desired steady state plasma level.

For Example:

A desired steady state plasma concentration of theophylline maybe 15 mg/L. The average half-life of theophylline is about 4 hr and the apparent volume of distribution is about 25 liter. What infusion rate is necessary?

First calculate kel from the t_1/2, kel = 0.693/4 = 0.17 hr^-1

then k0 = kel • V • Cp = 0.17 x 25 x 15 = 63.8 mg/hr

We would probably use an infusion of 60 mg/hr which would produce a Cp^ss value of:

Cp^ss = k0/(kel • V) = 60/(0.17 x 25) = 14.1 mg/L

Equation 6.2.4 can be used to calculate the steady state concentration after a continous infusion or the infusion rate constant required to achieve a required drug concentrstion.

Javascript Calculators using Equation 6.2.4

Calculator 6.2.3 Calculate Cp^ss Given k0, kel and V

Calculator 6.2.4 Calculate k0 required to give Cp^ss

For practice try calculating concentrations or required infusion rates. Compare your answers with the computer! These problems includes calculation of drug concentration or required infusion rates during an IV infusion or at steady state.

return to the Course index

This page was last modified: Sunday, 28th Jul 2024 at 4:49 pm

Privacy Statement - 25 May 2018

Material on this website should be used for Educational or Self-Study Purposes Only

Pharmacy Math Part Two
A selection of Pharmacy Math Problems