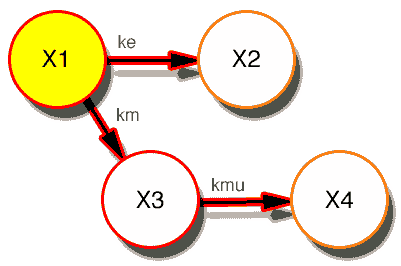
Figure 14.2.1 A Diagram Illustrating a One Compartment Model - IV Bolus
return to the Course index
previous | next

Figure 14.2.1 A Diagram Illustrating a One Compartment Model - IV Bolus
This model can be defined using both differential and integrated equations.
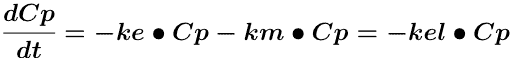
Equation 14.2.1 Differential Equation describing a One Compartment Model - IV Bolus
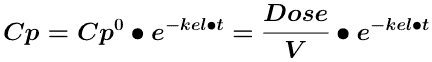
Equation 14.2.2 Integrated Equation describing a One Compartment Model - IV Bolus
or in clearance terms
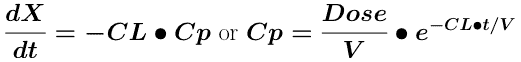
Equation 14.2.3 Equations describing a One Compartment Model - IV Bolus
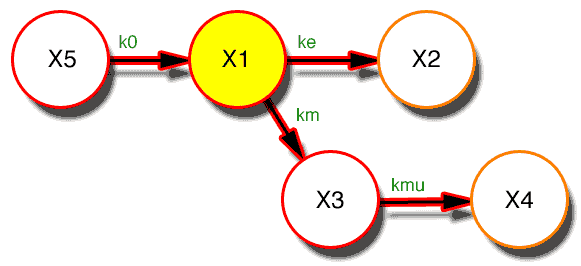
Figure 14.2.2 A Diagram Illustrating a One Compartment Model - IV Infusion
This model can be defined using both differential and integrated equations.
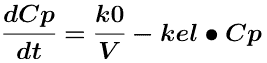
Equation 14.2.4 Differential Equation describing a One Compartment Model - IV Infusion
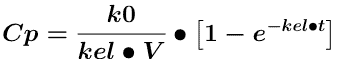
Equation 14.2.5 Integrated Equation describing a One Compartment Model - IV Infusion
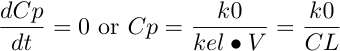
Equation 14.2.6 Equation describing a One Compartment Model - IV Infusion
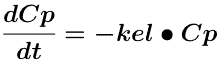
Equation 14.2.7 Differential Equation describing a One Compartment Model - IV Infusion
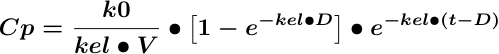
Equation 14.2.8 Integrated Equation describing a One Compartment Model - IV Infusion
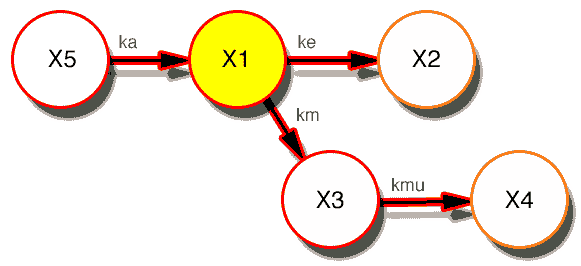
Figure 14.2.3 A Diagram Illustrating a One Compartment Model - Oral
This model can be defined using both differential and integrated equations.
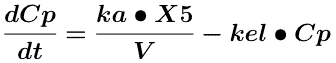
Equation 14.2.9 Differential Equation describing a One Compartment Model - Oral
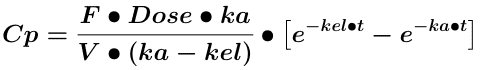
Equation 14.2.10 Integrated Equation describing a One Compartment Model - Oral
After a single IV bolus dose drug concentrations appear with an exponential decline on linear graph paper and a straight line on semi-log graph paper. With an IV infusion of duration T there is a steady increase to CpT followed by an abrupt exponential decline in concentration. After a single oral administration the curve around the peak concentration is smoother.

Figure 14.2.4 Linear Plot of Drug Concentration versus Time

Figure 14.2.5 Semi-log Plot of Drug Concentration versus Time
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2025 David W. A. Bourne (david@boomer.org)
 | Pharmacy Math Part Two A selection of Pharmacy Math Problems |
 |