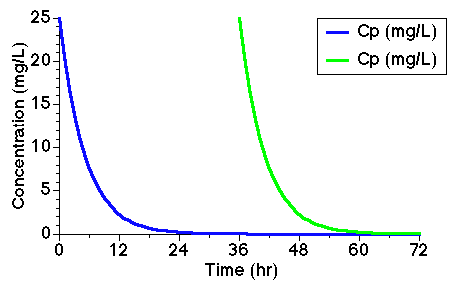
Figure 14.3.1 Drug Concentration after Two Independent IV Bolus Doses
return to the Course index
previous | next
Multiple dose administration is a very common method of drug administration. Up to this point we can calculate the drug concentration in plasma at any time after a single dose. We will continue now by looking at the equations for multiple dose administration.
We have already looked at the shape of the plasma concentration versus time curve following a single intravenous administration. If we assume instantaneous mixing we start off with an initial concentration, Cp0, calculated as Dose/V and then we have a fall in concentration with time controlled by the elimination rate constant.

Figure 14.3.1 Drug Concentration after Two Independent IV Bolus Doses
If the doses are given far enough apart then the concentration will have fallen to approximately zero before the next dose. There will then be no accumulation of drug in the body.
Material on this website should be used for Educational or Self-Study Purposes Only
Copyright © 2001 - 2026 David W. A. Bourne (david@boomer.org)
 | Pharmacy Math Part Two A selection of Pharmacy Math Problems |
 |